过拟合、欠拟合及其解决方案
模型选择、过拟合和欠拟合
训练误差和泛化误差
在解释上述现象之前,我们需要区分训练误差(training error)和泛化误差(generalization error)。通俗来讲,前者指模型在训练数据集上表现出的误差,后者指模型在任意一个测试数据样本上表现出的误差的期望,并常常通过测试数据集上的误差来近似。计算训练误差和泛化误差可以使用之前介绍过的损失函数,例如线性回归用到的平方损失函数和softmax回归用到的交叉熵损失函数。
模型选择
验证数据集
从严格意义上讲,测试集只能在所有超参数和模型参数选定后使用一次。不可以使用测试数据选择模型,如调参。由于无法从训练误差估计泛化误差,因此也不应只依赖训练数据选择模型。鉴于此,我们可以预留一部分在训练数据集和测试数据集以外的数据来进行模型选择。这部分数据被称为验证数据集,简称验证集(validation set)。例如,我们可以从给定的训练集中随机选取一小部分作为验证集,而将剩余部分作为真正的训练集。
K折交叉验证
由于验证数据集不参与模型训练,当训练数据不够用时,预留大量的验证数据显得太奢侈。一种改善的方法是K折交叉验证(K-fold cross-validation)。在K折交叉验证中,我们把原始训练数据集分割成K个不重合的子数据集,然后我们做K次模型训练和验证。每一次,我们使用一个子数据集验证模型,并使用其他K-1个子数据集来训练模型。在这K次训练和验证中,每次用来验证模型的子数据集都不同。最后,我们对这K次训练误差和验证误差分别求平均。
过拟合和欠拟合
接下来,我们将探究模型训练中经常出现的两类典型问题:
- 一类是模型无法得到较低的训练误差,我们将这一现象称作欠拟合(underfitting);
- 另一类是模型的训练误差远小于它在测试数据集上的误差,我们称该现象为过拟合(overfitting)。 在实践中,我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题,在这里我们重点讨论两个因素:模型复杂度和训练数据集大小。
模型复杂度
为了解释模型复杂度,我们以多项式函数拟合为例。给定一个由标量数据特征和对应的标量标签组成的训练数据集,多项式函数拟合的目标是找一个阶多项式函数
$$ \hat{y} = b + \sum_{k=1}^K x^k w_k $$
来近似$y$ 。在上式中,$w_k$是模型的权重参数,$b$是偏差参数。与线性回归相同,多项式函数拟合也使用平方损失函数。特别地,一阶多项式函数拟合又叫线性函数拟合。
给定训练数据集,模型复杂度和误差之间的关系:
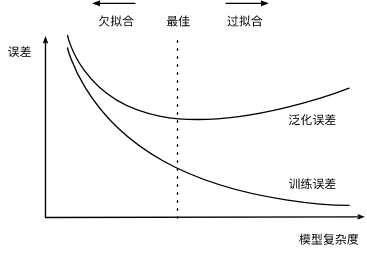
训练数据集大小
影响欠拟合和过拟合的另一个重要因素是训练数据集的大小。一般来说,如果训练数据集中样本数过少,特别是比模型参数数量(按元素计)更少时,过拟合更容易发生。此外,泛化误差不会随训练数据集里样本数量增加而增大。因此,在计算资源允许的范围之内,我们通常希望训练数据集大一些,特别是在模型复杂度较高时,例如层数较多的深度学习模型。
多项式函数拟合实验
1 | %matplotlib inline |
初始化模型参数
1 | n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5 |
定义、训练和测试模型
1 | def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None, |
三阶多项式函数拟合(正常)
1 | fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :], labels[:n_train], labels[n_train:]) |

线性函数拟合(欠拟合)
1 | fit_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train], labels[n_train:]) |

训练样本不足(过拟合)
1 | fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2], labels[n_train:]) |
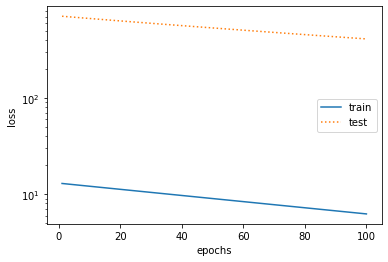
权重衰减
方法
权重衰减等价于$L_2$范数正则化(regularization)。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小,是应对过拟合的常用手段。
L2 范数正则化(regularization)
$L_2$范数正则化在模型原损失函数基础上添加$L_2$范数惩罚项,从而得到训练所需要最小化的函数。$L_2$范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以线性回归中的线性回归损失函数为例
$$ \ell(w_1, w_2, b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right)^2 $$
其中$w_1, w_2$是权重参数,$b$是偏差参数,样本$i$的输入为$x_1^{(i)}, x_2^{(i)}$,标签为$y^{(i)}$,样本数为$n$。将权重参数用向量$\boldsymbol{w} = [w_1, w_2]$表示,带有$L_2$范数惩罚项的新损失函数为
$$ \ell(w_1, w_2, b) + \frac{\lambda}{2n} |\boldsymbol{w}|^2, $$
其中超参数$\lambda > 0$。当权重参数均为0时,惩罚项最小。当$\lambda$较大时,惩罚项在损失函数中的比重较大,这通常会使学到的权重参数的元素较接近0。当$\lambda$设为0时,惩罚项完全不起作用。上式中$L_2$范数平方$|\boldsymbol{w}|^2$展开后得到$w_1^2 + w_2^2$。 有了$L_2$范数惩罚项后,在小批量随机梯度下降中,我们将线性回归一节中权重$w_1$和$w_2$的迭代方式更改为
$$
\begin{aligned} w_1 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\ w_2 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned}
$$
可见,范数正则化令权重和先自乘小于1的数,再减去不含惩罚项的梯度。因此,范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效。
高维线性回归实验从零开始的实现
下面,我们以高维线性回归为例来引入一个过拟合问题,并使用权重衰减来应对过拟合$p$。设数据样本特征的维度为$x_1, x_2, \ldots, x_p$。对于训练数据集和测试数据集中特征为的任一样本,我们使用如下的线性函数来生成该样本的标签:
$$
y = 0.05 + \sum_{i = 1}^p 0.01x_i + \epsilon
$$
其中噪声项$\epsilon$服从均值为0、标准差为0.01的正态分布。为了较容易地观察过拟合,我们考虑高维线性回归问题,如设维度$p=200$;同时,我们特意把训练数据集的样本数设低,如20。1
2
3
4
5
6
7
8
9%matplotlib inline
import torch
import torch.nn as nn
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__) # 1.3.0
初始化模型参数
与前面观察过拟合和欠拟合现象的时候相似,在这里不再解释。1
2
3
4
5
6
7
8
9
10
11
12
13n_train, n_test, num_inputs = 20, 100, 200
true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05
features = torch.randn((n_train + n_test, num_inputs))
labels = torch.matmul(features, true_w) + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]
# 定义参数初始化函数,初始化模型参数并且附上梯度
def init_params():
w = torch.randn((num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
定义L2范数惩罚项
1 | def l2_penalty(w): |
定义训练和测试
1 | batch_size, num_epochs, lr = 1, 100, 0.003 |
观察过拟合
1 | fit_and_plot(lambd=0) |
使用权重衰减
1 | fit_and_plot(lambd=3) |
简洁实现
1 | def fit_and_plot_pytorch(wd): |
丢弃法
多层感知机中神经网络图描述了一个单隐藏层的多层感知机。其中输入个数为4,隐藏单元个数为5,且隐藏单元$h_i$($i=1, \ldots, 5$)的计算表达式为
$$
h_i = \phi\left(x_1 w_{1i} + x_2 w_{2i} + x_3 w_{3i} + x_4 w_{4i} + b_i\right)
$$
这里是$\phi$激活函数,$x_1, \ldots, x_4$是输入,隐藏单元的权重参数为$w_{1i}, \ldots, w_{4i}$,偏差参数为$b_i$。当对该隐藏层使用丢弃法时,该层的隐藏单元将有一定概率被丢弃掉。设丢弃概率为$p$,那么有$p$的概率$h_i$会被清零,有$1-p$的概率$h_i$会除以$1-p$做拉伸。丢弃概率是丢弃法的超参数。具体来说,设随机变量$\xi_i$为0和1的概率分别$p$为和$1-p$。使用丢弃法时我们计算新的隐藏单元$h_i’$
$$
h_i’ = \frac{\xi_i}{1-p} h_i
$$
由于$E(\xi_i) = 1-p$,因此
$$
E(h_i’) = \frac{E(\xi_i)}{1-p}h_i = h_i
$$
即丢弃法不改变其输入的期望值。让我们对之前多层感知机的神经网络中的隐藏层使用丢弃法,一种可能的结果如图所示,其中$h_2$和$h_5$被清零。这时输出值的计算不再依赖$h_2$和$h_5$,在反向传播时,与这两个隐藏单元相关的权重的梯度均为0。由于在训练中隐藏层神经元的丢弃是随机的,即$h_1, \ldots, h_5$都有可能被清零,输出层的计算无法过度依赖$h_1, \ldots, h_5$中的任一个,从而在训练模型时起到正则化的作用,并可以用来应对过拟合。在测试模型时,我们为了拿到更加确定性的结果,一般不使用丢弃法

丢弃法从零开始的实现
1 | %matplotlib inline |
简洁实现
1 | net = nn.Sequential( |
总结
- 欠拟合现象:模型无法达到一个较低的误差
- 过拟合现象:训练误差较低但是泛化误差依然较高,二者相差较大
笔记整理
为什么优化器中只对权重参数设置衰减,而不对偏置参数设置衰减呢?
对偏置增加正则也是可以的,但是对偏置增加正则不会明显的产生很好的效果。而且偏置并不会像权重一样对数据非常敏感,所以不用担心偏置会学习到数据中的噪声。而且大的偏置也会使得我们的网络更加灵活,所以一般不对偏置做正则化。L2范数惩罚项通过惩罚绝对值较大的参数的方法来应对过拟合的。这里面的惩罚绝对值较大的参数是什么意思?
L2处理 权重会先自乘小于1的系数,再减去不含惩罚项的梯度;系数相等的情况下,绝对值较大的参数损失较大,故而惩罚较大。按照最开始的说法,训练集,测试集(用来测试训练成果),验证集(用来训练超参数或者选择模型),但K折交叉验证为什么只有k-1个训练和1个验证,没有测试集?“。在这K次训练和验证中,每次用来验证模型的子数据集都不同。最后,我们对这K次训练误差和验证误差分别求平均。”那么这里的k次训练误差是哪里来的呢?
正常的训练过程是分为训练数据和测试数据,但是如果只使用训练数据得到的模型效果不一定是最好的,所以在训练集中划分出验证集,训练集和验证集的划分有很多中,但是最常用的就是k折交叉验证,就是把训练数据分成k份,用其中的 k-1份训练模型,用剩下的一份来验证模型的泛化能力,循环操作,选择最佳的超参数组合,之后再用全部数据训练得到一个模型,再用测试数据来看模型的最终效果。有一个疑问。dropout(x,0.5)16个数按照0.5的概率丢弃,不应该是丢弃8个数字吗?是老师的口误吗?
丢弃率是指某个单元被丢弃(或者说被置为零)的概率。如丢弃率=0.5,表明每个单元都有50%的概率被置零,但各个单元之间是相互独立的。如,16个数(或者说16个单元)按照0.5概率丢弃,会出现16个数都被丢弃(或者16个数都被保留)的情况,概率为0.5^16;当然还有很多种被保留或丢弃的情况组合,最终的统计平均或者说期望是8个。dropout的时候为什么要进行1-p的拉伸?
假设dropout概率为p,那么每个节点被保留的概率是1-p
以p=0.3为例,假如某一个全连接层有10个输入节点
训练时启用dropout,因此理想情况是7个节点能够向后传递信息。
而实际使用时不用dropout,因此10个节点能向后传递信息。
因此输出节点接收到的信号强度是不一样的,为了平衡训练和预测时的这种量级差异。
可以选择在训练的时候,对每个输入节点进行 除(1-p) 的操作,来进行“拉伸”权重衰减可以有效处理过拟合的情况,这应该符合奥卡姆剃刀原理的吧?? 权重衰减可避免突出参数的负面干扰,而且经过数据验证也可看到这样确实有更好的拟合效果;但这样的结果是否与我们一直接触的大众数据有关呢,面对一些非常规的数据,比如说地震监测数据等,这种情况需要更显著地区段跳跃,那么这种处理方式还有效吗???
符合,引入正则项实际上是学习器的一种归纳偏好,即:选用尽可能简单的模型,避免过拟合,因为这样能够有更好的泛化性能。 这是一个增强泛化性能的通用的处理方式,当然如果你的模型如果本身准确率就不高,不会产生过拟合,那这种做法当然效果不好
梯度消失、梯度爆炸以及Kaggle房价预测
梯度消失和梯度爆炸
深度模型有关数值稳定性的典型问题是消失(vanishing)和爆炸(explosion)。
当神经网络的层数较多时,模型的数值稳定性容易变差。
假设一个层数为$L$的多层感知机的第$l$层$\boldsymbol{H}^{(l)}$的权重参数为$\boldsymbol{W}^{(l)}$,输出层$\boldsymbol{H}^{(l)}$的权重参数为$\boldsymbol{W}^{(l)}$。为了便于讨论,不考虑偏差参数,且设所有隐藏层的激活函数为恒等映射(identity mapping)$\phi(x) = x$。给定输入$X$,多层感知机的第$l$层的输出$\boldsymbol{H}^{(l)} = \boldsymbol{X} \boldsymbol{W}^{(1)} \boldsymbol{W}^{(2)} \ldots \boldsymbol{W}^{(l)}$。此时,如果层数$l$较大,$\boldsymbol{H}^{(l)}$的计算可能会出现衰减或爆炸。举个例子,假设输入和所有层的权重参数都是标量,如权重参数为0.2和5,多层感知机的第30层输出为输入$\boldsymbol{X}$分别与$0.2^{30} \approx 1 \times 10^{-21}$(消失)和$5^{30} \approx 9 \times 10^{20}$(爆炸)的乘积。当层数较多时,梯度的计算也容易出现消失或爆炸。
随机初始化模型参数
在神经网络中,通常需要随机初始化模型参数。下面我们来解释这样做的原因。
回顾多层感知机一节描述的多层感知机。为了方便解释,假设输出层只保留一个输出单元$o_1$(删去$o_2$和$o_3$以及指向它们的箭头),且隐藏层使用相同的激活函数。如果将每个隐藏单元的参数都初始化为相等的值,那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值,并传递至输出层。在反向传播中,每个隐藏单元的参数梯度值相等。因此,这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下,无论隐藏单元有多少,隐藏层本质上只有1个隐藏单元在发挥作用。因此,正如在前面的实验中所做的那样,我们通常将神经网络的模型参数,特别是权重参数,进行随机初始化。
Image Name
PyTorch的默认随机初始化
随机初始化模型参数的方法有很多。在线性回归的简洁实现中,我们使用torch.nn.init.normal_()使模型net的权重参数采用正态分布的随机初始化方式。不过,PyTorch中nn.Module的模块参数都采取了较为合理的初始化策略(不同类型的layer具体采样的哪一种初始化方法的可参考源代码),因此一般不用我们考虑。
Xavier随机初始化
还有一种比较常用的随机初始化方法叫作Xavier随机初始化。 假设某全连接层的输入个数为$a$,输出个数为$b$,Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布
$$
U\left(-\sqrt{\frac{6}{a+b}}, \sqrt{\frac{6}{a+b}}\right).
$$
它的设计主要考虑到,模型参数初始化后,每层输出的方差不该受该层输入个数影响,且每层梯度的方差也不该受该层输出个数影响。
考虑到环境因素的其他问题
协变量偏移
这里我们假设,虽然输入的分布可能随时间而改变,但是标记函数,即条件分布$P(y∣x)$不会改变。虽然这个问题容易理解,但在实践中也容易忽视。
想想区分猫和狗的一个例子。我们的训练数据使用的是猫和狗的真实的照片,但是在测试时,我们被要求对猫和狗的卡通图片进行分类。
cat cat dog dog
Image Name Image Name Image Name Image Name
测试数据:
cat cat dog dog
Image Name Image Name Image Name Image Name
显然,这不太可能奏效。训练集由照片组成,而测试集只包含卡通。在一个看起来与测试集有着本质不同的数据集上进行训练,而不考虑如何适应新的情况,这是不是一个好主意。不幸的是,这是一个非常常见的陷阱。
统计学家称这种协变量变化是因为问题的根源在于特征分布的变化(即协变量的变化)。数学上,我们可以说P(x)改变了,但P(y∣x)保持不变。尽管它的有用性并不局限于此,当我们认为x导致y时,协变量移位通常是正确的假设。
标签偏移
当我们认为导致偏移的是标签P(y)上的边缘分布的变化,但类条件分布是不变的P(x∣y)时,就会出现相反的问题。当我们认为y导致x时,标签偏移是一个合理的假设。例如,通常我们希望根据其表现来预测诊断结果。在这种情况下,我们认为诊断引起的表现,即疾病引起的症状。有时标签偏移和协变量移位假设可以同时成立。例如,当真正的标签函数是确定的和不变的,那么协变量偏移将始终保持,包括如果标签偏移也保持。有趣的是,当我们期望标签偏移和协变量偏移保持时,使用来自标签偏移假设的方法通常是有利的。这是因为这些方法倾向于操作看起来像标签的对象,这(在深度学习中)与处理看起来像输入的对象(在深度学习中)相比相对容易一些。
病因(要预测的诊断结果)导致 症状(观察到的结果)。
训练数据集,数据很少只包含流感p(y)的样本。
而测试数据集有流感p(y)和流感q(y),其中不变的是流感症状p(x|y)。
概念偏移
另一个相关的问题出现在概念转换中,即标签本身的定义发生变化的情况。这听起来很奇怪,毕竟猫就是猫。的确,猫的定义可能不会改变,但我们能不能对软饮料也这么说呢?事实证明,如果我们周游美国,按地理位置转移数据来源,我们会发现,即使是如图所示的这个简单术语的定义也会发生相当大的概念转变。
Image Name
美国软饮料名称的概念转变
如果我们要建立一个机器翻译系统,分布P(y∣x)可能因我们的位置而异。这个问题很难发现。另一个可取之处是P(y∣x)通常只是逐渐变化。
Kaggle房价预测
作为深度学习基础篇章的总结,我们将对本章内容学以致用。下面,让我们动手实战一个Kaggle比赛:房价预测。本节将提供未经调优的数据的预处理、模型的设计和超参数的选择。我们希望读者通过动手操作、仔细观察实验现象、认真分析实验结果并不断调整方法,得到令自己满意的结果。1
2
3
4
5
6
7
8
9
10import torch
import torch.nn as nn
import numpy as np
import pandas as pd
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__)
torch.set_default_tensor_type(torch.FloatTensor)
# 1.3.0
获取和读取数据集
比赛数据分为训练数据集和测试数据集。两个数据集都包括每栋房子的特征,如街道类型、建造年份、房顶类型、地下室状况等特征值。这些特征值有连续的数字、离散的标签甚至是缺失值“na”。只有训练数据集包括了每栋房子的价格,也就是标签。我们可以访问比赛网页,点击“Data”标签,并下载这些数据集。
我们将通过pandas库读入并处理数据。在导入本节需要的包前请确保已安装pandas库。 假设解压后的数据位于/home/kesci/input/houseprices2807/目录,它包括两个csv文件。下面使用pandas读取这两个文件。1
2test_data = pd.read_csv("/home/kesci/input/houseprices2807/house-prices-advanced-regression-techniques/test.csv")
train_data = pd.read_csv("/home/kesci/input/houseprices2807/house-prices-advanced-regression-techniques/train.csv")
训练数据集包括1460个样本、80个特征和1个标签。1
train_data.shape # (1460, 81)
测试数据集包括1459个样本和80个特征。我们需要将测试数据集中每个样本的标签预测出来。1
test_data.shape # (1459, 80)
让我们来查看前4个样本的前4个特征、后2个特征和标签(SalePrice):1
2
3
4
5
6train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]]
# Id MSSubClass MSZoning LotFrontage SaleType SaleCondition SalePrice
# 0 1 60 RL 65.0 WD Normal 208500
# 1 2 20 RL 80.0 WD Normal 181500
# 2 3 60 RL 68.0 WD Normal 223500
# 3 4 70 RL 60.0 WD Abnorml 140000
可以看到第一个特征是Id,它能帮助模型记住每个训练样本,但难以推广到测试样本,所以我们不使用它来训练。我们将所有的训练数据和测试数据的79个特征按样本连结。1
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))
预处理数据
我们对连续数值的特征做标准化(standardization):设该特征在整个数据集上的均值为,标准差为。那么,我们可以将该特征的每个值先减去再除以得到标准化后的每个特征值。对于缺失的特征值,我们将其替换成该特征的均值。1
2
3
4
5numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply
lambda x: (x - x.mean()) / (x.std()))
# 标准化后,每个数值特征的均值变为0,所以可以直接用0来替换缺失值
all_features[numeric_features] = all_features[numeric_features].fillna(0)
接下来将离散数值转成指示特征。举个例子,假设特征MSZoning里面有两个不同的离散值RL和RM,那么这一步转换将去掉MSZoning特征,并新加两个特征MSZoning_RL和MSZoning_RM,其值为0或1。如果一个样本原来在MSZoning里的值为RL,那么有MSZoning_RL=1且MSZoning_RM=0。1
2
3# dummy_na=True将缺失值也当作合法的特征值并为其创建指示特征
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape # (2919, 331)
可以看到这一步转换将特征数从79增加到了331。
最后,通过values属性得到NumPy格式的数据,并转成Tensor方便后面的训练。1
2
3
4n_train = train_data.shape[0]
train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float)
test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float)
train_labels = torch.tensor(train_data.SalePrice.values, dtype=torch.float).view(-1, 1)
训练模型
1 | loss = torch.nn.MSELoss() |
下面定义比赛用来评价模型的对数均方根误差。给定预测值和对应的真实标签,它的定义为
对数均方根误差的实现如下。1
2
3
4
5
6def log_rmse(net, features, labels):
with torch.no_grad():
# 将小于1的值设成1,使得取对数时数值更稳定
clipped_preds = torch.max(net(features), torch.tensor(1.0))
rmse = torch.sqrt(2 * loss(clipped_preds.log(), labels.log()).mean())
return rmse.item()
下面的训练函数跟本章中前几节的不同在于使用了Adam优化算法。相对之前使用的小批量随机梯度下降,它对学习率相对不那么敏感。我们将在之后的“优化算法”一章里详细介绍它。
1 | def train(net, train_features, train_labels, test_features, test_labels, |
K折交叉验证
我们在模型选择、欠拟合和过拟合中介绍了折交叉验证。它将被用来选择模型设计并调节超参数。下面实现了一个函数,它返回第i折交叉验证时所需要的训练和验证数据。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16def get_k_fold_data(k, i, X, y):
# 返回第i折交叉验证时所需要的训练和验证数据
assert k > 1
fold_size = X.shape[0] // k
X_train, y_train = None, None
for j in range(k):
idx = slice(j * fold_size, (j + 1) * fold_size)
X_part, y_part = X[idx, :], y[idx]
if j == i:
X_valid, y_valid = X_part, y_part
elif X_train is None:
X_train, y_train = X_part, y_part
else:
X_train = torch.cat((X_train, X_part), dim=0)
y_train = torch.cat((y_train, y_part), dim=0)
return X_train, y_train, X_valid, y_valid
在折交叉验证中我们训练次并返回训练和验证的平均误差
1 | def k_fold(k, X_train, y_train, num_epochs, |
模型选择
我们使用一组未经调优的超参数并计算交叉验证误差。可以改动这些超参数来尽可能减小平均测试误差。 有时候你会发现一组参数的训练误差可以达到很低,但是在折交叉验证上的误差可能反而较高。这种现象很可能是由过拟合造成的。因此,当训练误差降低时,我们要观察折交叉验证上的误差是否也相应降低。1
2
3
4
5
6
7
8
9k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr, weight_decay, batch_size)
print('%d-fold validation: avg train rmse %f, avg valid rmse %f' % (k, train_l, valid_l))
# fold 0, train rmse 0.241365, valid rmse 0.223083
# fold 1, train rmse 0.229118, valid rmse 0.267488
# fold 2, train rmse 0.232072, valid rmse 0.237995
# fold 3, train rmse 0.238050, valid rmse 0.218671
# fold 4, train rmse 0.231004, valid rmse 0.259185
# 5-fold validation: avg train rmse 0.234322, avg valid rmse 0.241284
预测并在Kaggle中提交结果
下面定义预测函数。在预测之前,我们会使用完整的训练数据集来重新训练模型,并将预测结果存成提交所需要的格式。
1 | def train_and_pred(train_features, test_features, train_labels, test_data, |
设计好模型并调好超参数之后,下一步就是对测试数据集上的房屋样本做价格预测。如果我们得到与交叉验证时差不多的训练误差,那么这个结果很可能是理想的,可以在Kaggle上提交结果。
1 | train_and_pred(train_features, test_features, train_labels, test_data, num_epochs, lr, weight_decay, batch_size) |
笔记整理
标签偏移指的是出现训练中不存在的标签,而圣诞礼物属于训练中存在的标签
请问反向传播是怎么回事?
将权重沿负梯度方向进行小步长的位移,可以逐渐的使loss函数下降,从而让模型具有好的效果。
反向传播其实就是从终点的loss往回回溯出每一个变量的梯度,从而好进行梯度下降的优化。
我看到梯度下降知识点的视频已放出,可以去学习一下,应该就对反向传播的意义有比较好的理解了。还是不懂标签偏移量和协变量偏移是什么?
标签偏移是在P(x∣y),在y的条件下x的概率,可以假设为y不变的情况下x的概率,而现实是y导致x发生了变化,而y是变化的所以就发生了标签偏移,因为y是标签。
而协变量偏移P(y∣x),同理可以假设为在x不变的情况下y的概率,而现实是x发生了变化导致y发生了变化,所以就发生了协变量偏移,x为变量。在反向传播中,每个隐藏单元的参数梯度值相等,这是为什么呢?
算出来相等那就确实相等,不是一定会相等