Lingmoumou's Blog

きっといつかって愿うまま

0%

Day1 机器学习概述

发表于 更新于 分类于 ，

任务

理论部分

  • 机器学习介绍：机器学习是什么，怎么来的，理论基础是什么，为了解决什么问题。
  • 机器学习分类：
    • 按学习方式分：有监督、无监督、半监督
    • 按任务类型分：回归、分类、聚类、降维 生成模型与判别模型
  • 机器学习方法三要素：
    • 模型
    • 策略：损失函数
    • 算法：梯度下降法、牛顿法、拟牛顿法
    • 模型评估指标：R2、RMSE、accuracy、precision、recall、F1、ROC、AUC、Confusion Matrix
    • 复杂度度量：偏差与方差、过拟合与欠拟合、结构风险与经验风险、泛化能力、正则化
    • 模型选择：正则化、交叉验证
    • 采样：样本不均衡
    • 特征处理：归一化、标准化、离散化、one-hot编码
    • 模型调优：网格搜索寻优、随机搜索寻优

机器学习综述

2016年3月，阿尔法围棋与围棋世界冠军、职业九段棋手李世石进行围棋人机大战，以4比1的总比分获胜。深度学习开始进行大众的视野中。深度学习其实是机器学习的一个分支,我们今天来看看机器学习是什么。机器学习是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。它是人工智能的核心，是使计算机具有智能的根本途径。

机器学习的发展

其中，机器学习（Machine Learning）的各个阶段发展历程列表如下。



















时间段机器学习理论代表性成果
二十世纪五十年代初人工智能研究处于推理期A. Newell和H. Simon的“逻辑理论家”（Logic Theorist）程序证明了数学原理，以及此后的“通用问题求解”（General Problem Solving）程序。
已出现机器学习的相关研究1952年，阿瑟·萨缪尔（Arthur Samuel）在IBM公司研制了一个西洋跳棋程序，这是人工智能下棋问题的由来。
二十世纪五十年代中后期开始出现基于神经网络的“连接主义”（Connectionism）学习F. Rosenblatt提出了感知机（Perceptron），但该感知机只能处理线性分类问题，处理不了“异或”逻辑。还有B. Widrow提出的Adaline。
二十世纪六七十年代基于逻辑表示的“符号主义”（Symbolism）学习技术蓬勃发展P. Winston的结构学习系统，R. S. Michalski的基于逻辑的归纳学习系统，以及E. B. Hunt的概念学习系统。
以决策理论为基础的学习技术 
强化学习技术N. J. Nilson的“学习机器”。
统计学习理论的一些奠基性成果支持向量，VC维，结构风险最小化原则。
二十世纪八十年代至九十年代中期机械学习（死记硬背式学习）
示教学习（从指令中学习）
类比学习（通过观察和发现学习）
归纳学习（从样例中学习）		学习方式分类
从样例中学习的主流技术之一：（1）符号主义学习
（2）基于逻辑的学习		（1）决策树（decision tree）。
（2）归纳逻辑程序设计（Inductive Logic Programming, ILP）具有很强的知识表示能力，可以较容易地表达出复杂的数据关系，但会导致学习过程面临的假设空间太大，复杂度极高，因此，问题规模稍大就难以有效地进行学习。
从样例中学习的主流技术之二：基于神经网络的连接主义学习1983年，J. J. Hopfield利用神经网络求解“流动推销员问题”这个NP难题。1986年，D. E. Rumelhart等人重新发明了BP算法，BP算法一直是被应用得最广泛的机器学习算法之一。
二十世纪八十年代是机器学习成为一个独立的学科领域，各种机器学习技术百花初绽的时期连接主义学习的最大局限是“试错性”，学习过程涉及大量参数，而参数的设置缺乏理论指导，主要靠手工“调参”，参数调节失之毫厘，学习结果可能谬以千里。
二十世纪九十年代中期统计学习（Statistical Learning）支持向量机（Support Vector Machine，SVM），核方法（Kernel Methods）。
二十一世纪初至今深度学习（Deep Learning）深度学习兴起的原因有二：数据量大，机器计算能力强。

机器学习分类 ^6

  1. 监督学习
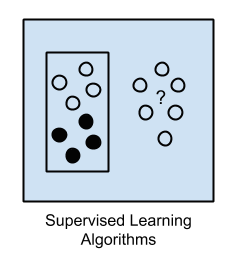
    监督学习是指利用一组已知类别的样本调整分类器的参数，使其达到所要求性能的过程，也称为监督训练或有教师学习。在监督学习的过程中会提供对错指示，通过不断地重复训练，使其找到给定的训练数据集中的某种模式或规律，当新的数据到来时，可以根据这个函数预测结果。监督学习的训练集要求包括输入和输出，主要应用于分类和预测。
    Supervised Learning

  2. 非监督学习
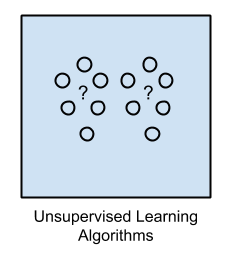
    与监督学习不同，在非监督学习中，无须对数据集进行标记，即没有输出。其需要从数据集中发现隐含的某种结构，从而获得样本数据的结构特征，判断哪些数据比较相似。因此，非监督学习目标不是告诉计算机怎么做，而是让它去学习怎样做事情。
    Unsupervised Learning

  3. 半监督学习
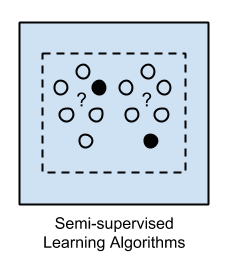
    半监督学习是监督学习和非监督学习的结合，其在训练阶段使用的是未标记的数据和已标记的数据，不仅要学习属性之间的结构关系，也要输出分类模型进行预测。
    Semi-Supervised Learning

  4. 强化学习
    强化学习（Reinforcement Learning, RL），又称再励学习、评价学习或增强学习，是机器学习的范式和方法论之一，用于描述和解决智能体（agent）在与环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题。

机器学习模型

机器学习 = 数据（data） + 模型（model） + 优化方法（optimal strategy）

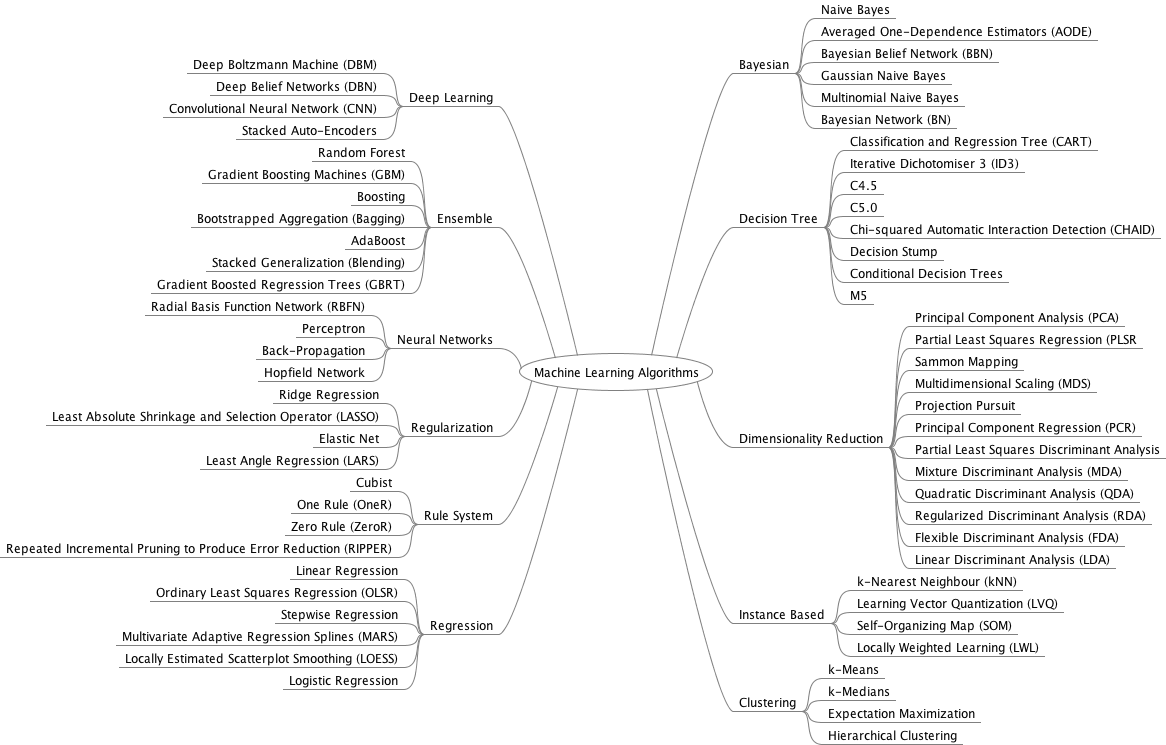
机器学习的算法导图

机器学习的注意事项

常见的机器学习算法

  1. Linear Algorithms
    1. Linear Regression
    2. Lasso Regression
    3. Ridge Regression
    4. Logistic Regression
  2. Decision Tree
    1. ID3
    2. C4.5
    3. CART
  3. SVM
  4. Naive Bayes Algorithms
    1. Naive Bayes
    2. Gaussian Naive Bayes
    3. Multinomial Naive Bayes
    4. Bayesian Belief Network (BBN)
    5. Bayesian Network (BN)
  5. kNN
  6. Clustering Algorithms
    1. k-Means
    2. k-Medians
    3. Expectation Maximisation (EM)
    4. Hierarchical Clustering
  7. K-Means
  8. Random Forest
  9. Dimensionality Reduction Algorithms
  10. Gradient Boosting algorithms
    1. GBM
    2. XGBoost
    3. LightGBM
    4. CatBoost
  11. Deep Learning Algorithms
    1. Convolutional Neural Network (CNN)
    2. Recurrent Neural Networks (RNNs)
    3. Long Short-Term Memory Networks (LSTMs)
    4. Stacked Auto-Encoders
    5. Deep Boltzmann Machine (DBM)
    6. Deep Belief Networks (DBN)

机器学习损失函数 ^8

  1. 0-1损失函数（0-1 loss function）
    $$
    L(y,f(x)) =
    \begin{cases}
    0, & \text{y = f(x)} \
    1, & \text{y $\neq$ f(x)}
    \end{cases}
    $$
    也就是说，当预测错误时，损失函数为1，当预测正确时，损失函数值为0。该损失函数不考虑预测值和真实值的误差程度。只要错误，就是1。

  2. 绝对值损失函数（absolute loss function）
    $$
    L(y,f(x))=|y-f(x)|
    $$
    该损失函数的意义和上面差不多，只不过是取了绝对值而不是求绝对值，差距不会被平方放大。

  3. 平方损失函数（quadratic loss function）
    $$
    L(y,f(x))=(y-f(x))^2
    $$
    是指预测值与实际值差的平方。

  4. log对数损失函数（logarithmic loss function）
    $$
    L(y,f(x))=log(1+e^{-yf(x)})
    $$
    这个损失函数就比较难理解了。事实上，该损失函数用到了极大似然估计的思想。P(Y|X)通俗的解释就是：在当前模型的基础上，对于样本X，其预测值为Y，也就是预测正确的概率。由于概率之间的同时满足需要使用乘法，为了将其转化为加法，我们将其取对数。最后由于是损失函数，所以预测正确的概率越高，其损失值应该是越小，因此再加个负号取个反。

  5. 指数损失函数
    $$
    L(y,f(x))=exp(-yf(x))
    $$

  6. Hinge损失函数
    Hinge loss一般分类算法中的损失函数，尤其是SVM，其定义为：
    $$
    L(w,b)=max{0,1-yf(x)}
    $$
    其中$$ y=+1 $$或$$ y=−1 $$ ，$$ f(x)=wx+b $$，当为SVM的线性核时。

机器学习优化方法

梯度下降是最常用的优化方法之一，它使用梯度的反方向$\nabla_\theta J(\theta)$更新参数$\theta$，使得目标函数$J(\theta)$达到最小化的一种优化方法，这种方法我们叫做梯度更新。

  1. (全量)梯度下降
    $$
    \theta=\theta-\eta\nabla_\theta J(\theta)
    $$
  2. 随机梯度下降
    $$
    \theta=\theta-\eta\nabla_\theta J(\theta;x^{(i)},y^{(i)})
    $$
  3. 小批量梯度下降
    $$
    \theta=\theta-\eta\nabla_\theta J(\theta;x^{(i:i+n)},y^{(i:i+n)})
    $$
  4. 引入动量的梯度下降
    $$
    \begin{cases}
    v_t=\gamma v_{t-1}+\eta \nabla_\theta J(\theta) \
    \theta=\theta-v_t
    \end{cases}
    $$
  5. 自适应学习率的Adagrad算法
    $$
    \begin{cases}
    g_t= \nabla_\theta J(\theta) \
    \theta_{t+1}=\theta_{t,i}-\frac{\eta}{\sqrt{G_t+\varepsilon}} \cdot g_t
    \end{cases}
    $$
  6. 牛顿法
    $$
    \theta_{t+1}=\theta_t-H^{-1}\nabla_\theta J(\theta_t)
    $$
    其中:
    $t$: 迭代的轮数
    $\eta$: 学习率
    $G_t$: 前t次迭代的梯度和
    $\varepsilon:$很小的数,防止除0错误
    $H$: 损失函数相当于$\theta$的Hession矩阵在$\theta_t$处的估计

机器学习的评价指标 ^8

  1. 均方误差 MSE(Mean Squared Error)
    $$
    MSE(y,f(x))=\frac{1}{N}\sum_{i=1}^{N}(y-f(x))^2
    $$
    均方误差是指参数估计值与参数真值之差平方的期望值; MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。（ $ i $表示第$ i $个样本，$ N $ 表示样本总数）
    通常用来做回归问题的代价函数。

  2. 平均绝对误差 MAE(Mean Absolute Error)
    $$
    MSE(y,f(x))=\frac{1}{N}\sum_{i=1}^{N}|y-f(x)|
    $$
    平均绝对误差是绝对误差的平均值 ，平均绝对误差能更好地反映预测值误差的实际情况。
    通常用来作为回归算法的性能指标。

  3. 均方根误差 RMSE(Root Mean Squard Error)
    $$
    RMSE(y,f(x))=\frac{1}{1+MSE(y,f(x))}
    $$
    均方根误差是均方误差的算术平方根，能够直观观测预测值与实际值的离散程度。
    通常用来作为回归算法的性能指标。

  4. Top-k准确率
    $$
    Top_k(y,pre_y)=\begin{cases}
    1, {y \in pre_y} \
    0, {y \notin pre_y}
    \end{cases}
    $$

  5. 混淆矩阵 [9]







    混淆矩阵Predicted as PositivePredicted as Negative
    Labeled as PositiveTrue Positive(TP)False Negative(FN)
    Labeled as NegativeFalse Positive(FP)True Negative(TN)

    • 真正例(True Positive, TP):真实类别为正例, 预测类别为正例
    • 假负例(False Negative, FN): 真实类别为正例, 预测类别为负例
    • 假正例(False Positive, FP): 真实类别为负例, 预测类别为正例
    • 真负例(True Negative, TN): 真实类别为负例, 预测类别为负例
    • 真正率(True Positive Rate, TPR): 被预测为正的正样本数 / 正样本实际数
      $$
      TPR=\frac{TP}{TP+FN}
      $$

    • 假负率(False Negative Rate, FNR): 被预测为负的正样本数/正样本实际数
      $$
      FNR=\frac{FN}{TP+FN}
      $$

    • 假正率(False Positive Rate, FPR): 被预测为正的负样本数/负样本实际数，
      $$
      FPR=\frac{FP}{FP+TN}
      $$

    • 真负率(True Negative Rate, TNR): 被预测为负的负样本数/负样本实际数，
      $$
      TNR=\frac{TN}{FP+TN}
      $$
    • 准确率(Accuracy)
      $$
      ACC=\frac{TP+TN}{TP+FN+FP+TN}
      $$
    • 精准率
      $$
      P=\frac{TP}{TP+FP}
      $$
    • 召回率
      $$
      R=\frac{TP}{TP+FN}
      $$
    • F1-Score
      $$
      \frac{2}{F_1}=\frac{1}{P}+\frac{1}{R}
      $$
    • ROC
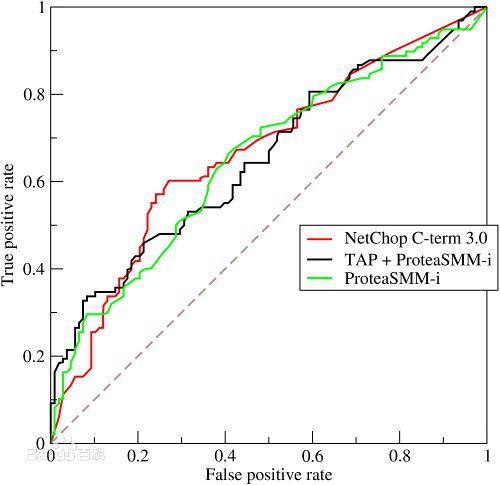
      ROC曲线的横轴为“假正例率”，纵轴为“真正例率”。以FPR为横坐标，TPR为纵坐标，那么ROC曲线就是改变各种阈值后得到的所有坐标点 (FPR,TPR) 的连线，画出来如下。红线是随机乱猜情况下的ROC，曲线越靠左上角，分类器越佳。

    • AUC(Area Under Curve)
      AUC就是ROC曲线下的面积。真实情况下，由于数据是一个一个的，阈值被离散化，呈现的曲线便是锯齿状的，当然数据越多，阈值分的越细，”曲线”越光滑。

      用AUC判断分类器（预测模型）优劣的标准:

      • AUC = 1 是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器.
      • 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值.
      • AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测.

机器学习模型选择

  1. 交叉验证
    所有数据分为三部分：训练集、交叉验证集和测试集。交叉验证集不仅在选择模型时有用，在超参数选择、正则项参数 [公式] 和评价模型中也很有用。

  2. k-折叠交叉验证

    • 假设训练集为S ，将训练集等分为k份:${S_1, S_2, …, S_k}$。
    • 然后每次从集合中拿出k-1份进行训练
    • 利用集合中剩下的那一份来进行测试并计算损失值
    • 最后得到k次测试得到的损失值，并选择平均损失值最小的模型

  3. Bias与Variance，欠拟合与过拟合 ^12
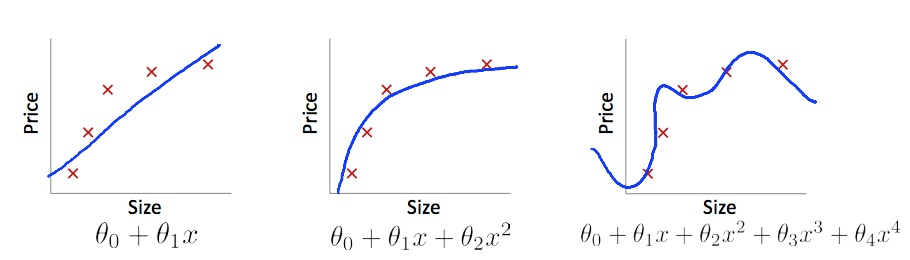
    如下图，针对同一组数据的三种模型，可以看出来中间的模型可以更好的表现数据，其中左边的模型一般称为欠拟合，右边的模型称为过拟合。

    欠拟合一般表示模型对数据的表现能力不足，通常是模型的复杂度不够，并且Bias高，训练集的损失值高，测试集的损失值也高.
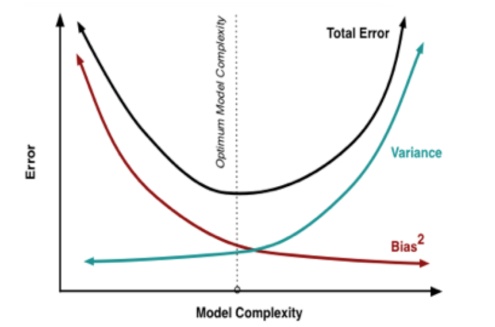
    过拟合一般表示模型对数据的表现能力过好，通常是模型的复杂度过高，并且Variance高，训练集的损失值低，测试集的损失值高.


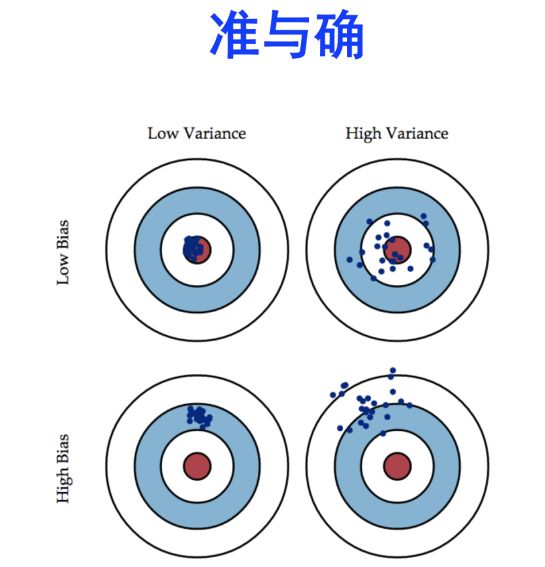
    Bias描述的是模型与数据表现的真实情况的差别，Variance描述的是我们的假设与最好的假设之间的差别。

  4. 解决方法

    • 增加训练样本: 解决高Variance情况
    • 减少特征维数: 解决高Variance情况
    • 增加特征维数: 解决高Bias情况
    • 增加模型复杂度: 解决高Bias情况
    • 减小模型复杂度: 解决高Variance情况

机器学习参数调优

  1. 网格搜索
    一种调参手段；穷举搜索：在所有候选的参数选择中，通过循环遍历，尝试每一种可能性，表现最好的参数就是最终的结果

  2. 随机搜索
    与网格搜索相比，随机搜索并未尝试所有参数值，而是从指定的分布中采样固定数量的参数设置。它的理论依据是，如果随即样本点集足够大，那么也可以找到全局的最大或最小值，或它们的近似值。通过对搜索范围的随机取样，随机搜索一般会比网格搜索要快一些。

  3. 贝叶斯优化算法
    贝叶斯优化用于机器学习调参由J. Snoek(2012)提出，主要思想是，给定优化的目标函数(广义的函数，只需指定输入和输出即可，无需知道内部结构以及数学性质)，通过不断地添加样本点来更新目标函数的后验分布(高斯过程,直到后验分布基本贴合于真实分布。简单的说，就是考虑了上一次参数的信息，从而更好的调整当前的参数。

参考文献